milimagnet.blogg.se - Solving systems by graphing

#Solving systems by graphing professional

#Solving systems by graphing professional

Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage.

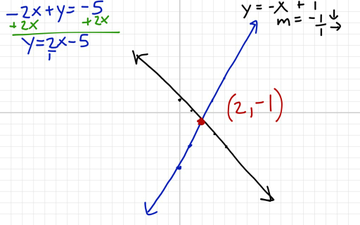
Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Therefore, we tend only to use the method of solving by graphing when we can employ a graphing calculator, as the other methods such as substitution, elimination, and row reduction are infinitely more accurate and efficient.īut as it’s important to visually understand what is happening when we solve a system (i.e., a picture is worth a thousand words) beginning our unit on solving systems by graphing is the logical first step.Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20. Graphing by hand isn’t very precise, and it can be tedious. While the steps for solving systems graphically are easy to follow, the process does have some pitfalls. This is why systems of equations are also called simultaneous equations. This means that a system of two equations imposes two conditions on the variables at the same time, meaning we are looking for when both equations have the same x value and the same y value at the same moment. Remember that in a system of two equations each equation contains two variables, x and y. If there are no solutions, then it is deemed inconsistent. If a system has one or an infinite number of solutions, then it is considered a consistent system. If the lines coincide, meaning they are the same line, there are an infinite number of solutions. If the lines are parallel, there is no solution. If the lines intersect, the coordinates of the point of intersection give the solution to the system.

Sketch the graph of each linear equation in the same coordinate plane. System of Linear Equations A set of two or more linear equations in the same variables Example: x + y 7 Equation 1 2x 3y Equation 2 Solution of a.

Transform both equations into Slope-Intercept Form.

Graph the second equation on the same rectangular coordinate system. Sketch the possible options for intersection. In fact, the whole graphic method process can be boiled down to three simple steps: Solve a system of nonlinear equations by graphing. As we saw in the previous chapter, if a point satises an equation, then that point lies on the graph of the equation. To solve a system of linear equations by graphing we simply graph both equations in the same coordinate plane, as Math Planet accurately states, and we identify the point where the two lines intersect. In this section we introduce a graphical technique for solving systems of two linear equations in two unknowns. Now there are several ways for us to solve a system of equations to find the intersection point, and this lesson is our first method – Solving Systems of Equations by Graphing. The first step is to graph each of the given equations, then find the point of intersection of the two lines, which is the solution to the system of equations. In other words, we are trying to find the point of intersection! Well, solving a system of linear equations is about finding what all of the equations have in common.

Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)